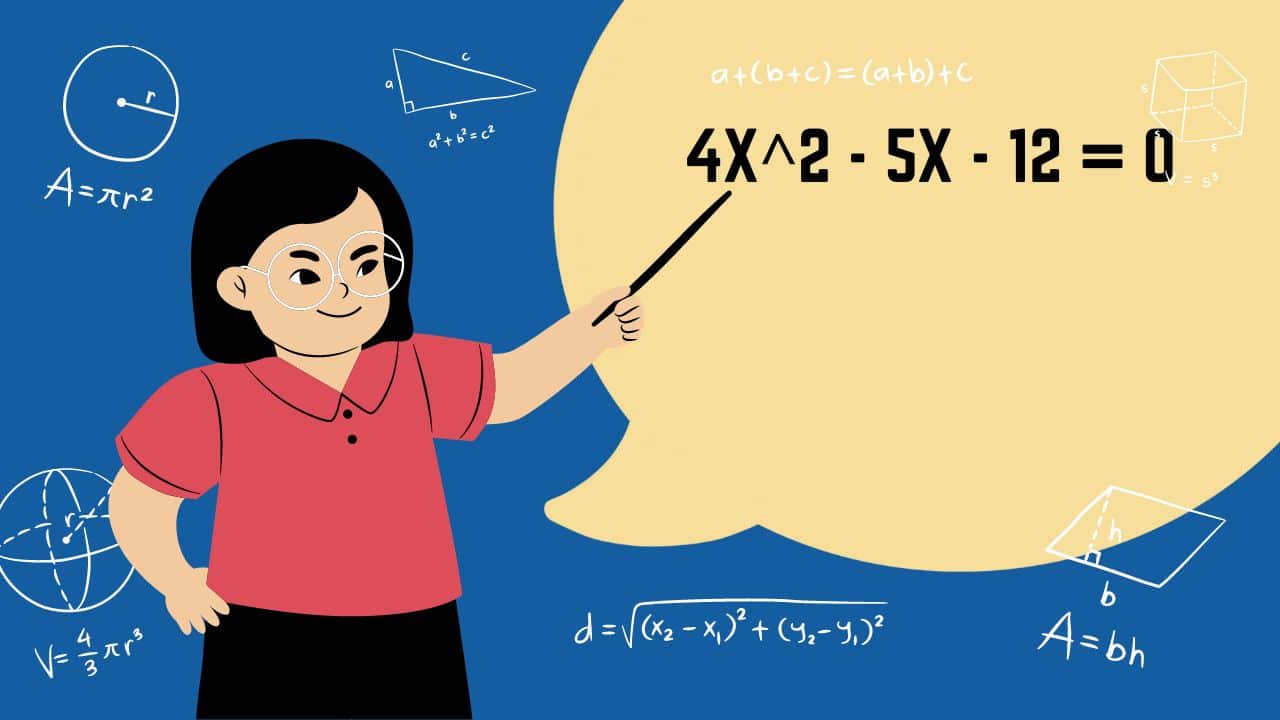Quadratic equations can be tough. Many students struggle to solve them, especially when faced with complex forms like 4x ^ 2 – 5x – 12 = 0. This equation looks daunting at first glance.
The quadratic formula is a powerful tool for solving such equations. It works for any quadratic in the form ax^2 + bx + c = 0. Our article will show you how to apply this formula to 4x ^ 2 – 5x – 12 = 0.
You’ll learn to find its roots step-by-step. Get ready to master this equation.
Solving the Quadratic Equation: 4x ^ 2 – 5x – 12 = 0
To solve this quadratic equation, we’ll use the quadratic formula. It’s a handy tool that works for any quadratic equation in the form ax^2 + bx + c = 0. Let’s plug in our values and crunch the numbers.
Apply the quadratic formula
The quadratic formula solves equations like 4x ^ 2 – 5x – 12 = 0. It’s X = (-B ± √(B^2 – 4AC)) / 2A, where A = 4, B = -5, and C = -12. Plug these values in: X = (5 ± √(25 + 192)) / 8.
Simplify to get X = (5 ± √217) / 8. This yields two solutions: (5 + √217) / 8 and (5 – √217) / 8.
The formula works for all quadratic equations, even those that can’t be factored. It’s faster than completing the square for complex problems. The discriminant (B^2 – 4AC) determines the nature of the roots – real, rational, or complex.
Calculate the discriminant
The discriminant reveals crucial information about a quadratic equation’s roots. For the equation 4x ^ 2 – 5x – 12 = 0, we calculate it using D = b^2 – 4ac. Plugging in a = 4, b = -5, and c = -12 gives us D = (-5)^2 – 4(4)(-12) = 25 + 192 = 217.
This positive value indicates two distinct real roots exist for this equation. Knowing the discriminant helps predict solution types without solving the full equation.
Analysis of the Equation’s Roots
The roots of this equation reveal its behavior. They show where the parabola crosses the x-axis.
Determine the nature of the roots based on the discriminant
The discriminant reveals crucial info about quadratic equation roots. In this case, the discriminant equals 217 – a positive number. Positive discriminants signal two distinct real roots. Real roots mean the parabola intersects the x-axis at two points. These intersection points represent the equation’s solutions on a graph.Additionally, you can also read about- 99Math Games.
Facts about Solving the Quadratic Equation
- The quadratic formula is X = (-B ± √(B^2 – 4AC)) / 2A.
- Solutions using the quadratic formula are:
- x = (5 + √217) / 8
- x = (5 – √217) / 8
- The values of a, b, and c are a = 4, b = -5, c = -12.
- Other ways to solve quadratic equations include using the quadratic formula and completing the square.
- Completing the square involves creating a perfect square trinomial and solving using the square root principle.
Facts about Calculate the discriminant
- The discriminant (D) is calculated to be 217.
- The formula for the discriminant is D = b^2 – 4ac.
- The discriminant is calculated based on the values a = 4, b = -5, and c = -12.
- The discriminant can be positive, negative, or zero, which corresponds to different types of roots
Takeaways
Mastering quadratic equations opens doors to advanced math concepts. This equation, 4x ^ 2 – 5x – 12 = 0, showcases real, distinct roots. Students gain valuable problem-solving skills through practice.
Applying these techniques builds confidence in tackling complex mathematical challenges. Quadratic equations serve as stepping stones to higher-level algebra and calculus.
References
- https://byjus.com/maths/quadratic-formula/
- http://readwithus.org.uk/solve-4x-2-5x-12-0 (2023-08-12)
- https://byjus.com/discriminant-calculator/
- https://www.proprep.com/questions/how-do-you-solve-the-equation-4x-2-5x-12-0
- https://www.mathway.com/popular-problems/Algebra/892544
- https://athometutoringservices.com/how-to-determine-nature-of-roots-quadratic-equations/